中文标题：Capsules网络与动态路由
英文标题：Dynamic Routing Between Capsules
发布平台：NIPS
Advances in neural information processing systems
发布日期：2017-01-01
引用量（非实时）：4433
DOI：缺失
作者：Sara Sabour, Nicholas Frosst, Geoffrey E Hinton
文章类型：conferencePaper
品读时间：2022-03-29 14:35
1 文章萃取
1.1 核心观点
胶囊是一组神经元构成的活跃向量，用于代表特定类型实体的实例化参数。向量的方向表示实体的具体实例化参数，向量的长度表示实体存在的概率。本文提出一种动态路由机制，实现低层胶囊向高层胶囊的组成，使得模型具备了对图像进行层次抽象的能力。相比于卷积神经网络，胶囊模型在MNIST上达到了更出色的精准度和稳健性，并且在图像分割方面表现异常出彩。
1.2 综合评价
- 通过动态路由机制，从神经网络中抽取解析树（整体与部分的层次关系）
- 严谨的实验展现出了优越的稳健性和泛化能力和巨大潜力
- 打破了梯度下降法的垄断局面，给神经网络提供了很多新的思路
- 借助无监督的自编码器机制，加快了模型对于实体的实例参数化过程
- 胶囊网络在大规模数据集上效率较低，表现较差；由于过度关注于全局信息，在背景复杂的情况时，效果会有所下降
1.3 主观评分：⭐⭐⭐⭐⭐
前言：从最初的图像解析到后来的自编码器的改造，作者一直专注于从更合理的视觉机制出发，发掘图像中整体与部分的空间关系。伴随着神经网络的逐步兴起，作者将这种思想融入到了卷积神经网络中，通过构建胶囊结构实现了对池化层的替代，并借助动态路由机制打破了千篇一律梯度下降的局面，这种将想法逐步落实的过程真的非常的美丽，本文的最终模型结构可能尚存在很多生涩的地方，但背后的想法是非常值得借鉴的，这种思路就像是一种在萌芽的种子，谁也不知道最后会生长出怎样的参天大树。
2 精读笔记
2.1 背景介绍
人类观察到的图像时，会自动忽略不相干的信息，并仔细确定一系列的固定点，以确保这部分光学信息能够以最高分辨率进行处理。
本文假设图像中的固定点都会通过多层神经网络构建一种解析树（从网到树是一个类似于剪枝的筛选过程）：每一层的神经元被分成多个神经元组，每个组被称为“胶囊（$Capsules$）”，解析树的每个节点就是一个活跃的$Capsule$。通过一个迭代路由的过程，每个活跃$Capsule$都会选择下一层的某个$Capsule$作为其在树中的父节点。而这种树形结构将会是获取图像层次抽象信息的关键。
一个活跃的$Capsule$是描述图像中的特定实体的实例化参数，参数向量的方向表示实体的属性：比如姿态（大小、位置、方向）、变形、反光、纹理等；参数向量的模长表示实体存在的概率，而本文使用以下函数确保向量的模长小于1： $$squshing(x)=\frac{||x||^2}{1+||x||^2}\frac{x}{||x||}$$ 其中前一项是对向量模长的压缩（这种压缩方式会减弱模长接近0时的输入向量的压缩，而增强模长过高时的输入向量的压缩），后一项是保留方向的单位向量
知识补充：函数$y=\frac{x^2}{a+x^2}$在$a=2,1,0.5,0.1$时的函数图像
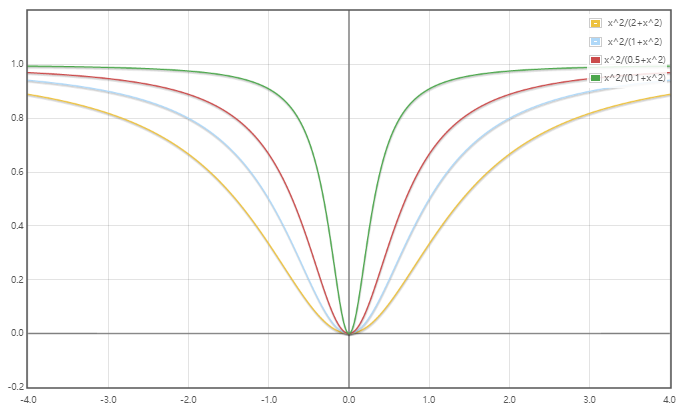
考虑卷积神经网络，多层次的卷积层实现了特征从简单和复杂的层次抽象，这一点值得借鉴；而池化层通过选取最值的方式筛选显著特征，虽然简单有效，但是过于粗暴，舍弃了很多有效的信息。$Capsule$需要取长补短，保留层次的结构特性并舍弃过于粗暴的特征筛选方法。
$Capsule$借助动态路由机制实现了对池化层的上位替代，动态路由机制的主要目的是实现底层$Capsule$的合理组合，用形成上层$Capsule$（举例来说，眼皮上的毛发是指眉毛，而嘴巴下的毛发是指胡子，眉毛和胡子又都是脸的组成部分，而不是腿的组成部分）。每一层都通过动态路由机制实现了关联与区分，这样就自然实现了从神经网络到解析树的内在转变。
2.2 算法细节
理解$Capsule$的思想后，就能发现实现$Capsule$网络的方法是很多的，而本文的目的不在于探究所有可能的方法，所以只是用较简单的方式展现$Capsule$的威力
2.2.1 Capsule输入与输出
不同于普通的神经元，每个$Capsule$的输入和输出都是向量，现在假设第$l$层的第$i$个$Capsule$的输出向量为$u_i$，第$l+1$层的第$j$个$Capsule$的输出向量为$v_j$，则从$Capsule_i$到$Capsule_j$的计算过程如下：
- 将$Capsule_i$的输出向量$u_i$与权重矩阵（权重矩阵可以理解为一种仿射变换）相乘，得到预测向量（Prediction Vector）：$\hat{u}{j|i}=W{ij}u_i$
- 通过动态路由机制，计算得到耦合系数$b_{ij}$，耦合系数描述了$Capsule_i$和$Capsule_j$之间的认同度（Agreement），用于构建底层特征与高层特征的组成关系
- 归一化耦合系数，确保$Capsule_j$与$l$层的所有$Capsule$的耦合系数和为1：$$c_{ij}=\frac{exp(b_ij)}{\Sigma_kexp(b_{ik})}$$
- 汇总第$l$层所有预测向量，以耦合系数为权重，求和得到$Capsule_j$的输入向量$s_j$：$$s_j=\Sigma_ic_{ij}\cdot \hat{u}_{j|i}$$
- 对输入变量进行非线性压缩（Squashing），得到$Capsule_j$的输出向量为$v_j$：$$v_j=\frac{||s_j||^2}{1+||s_j||^2}\frac{s_j}{||s_j||}$$
$Capsule$（向量入、向量出） VS 神经元（标量入、标量出）：
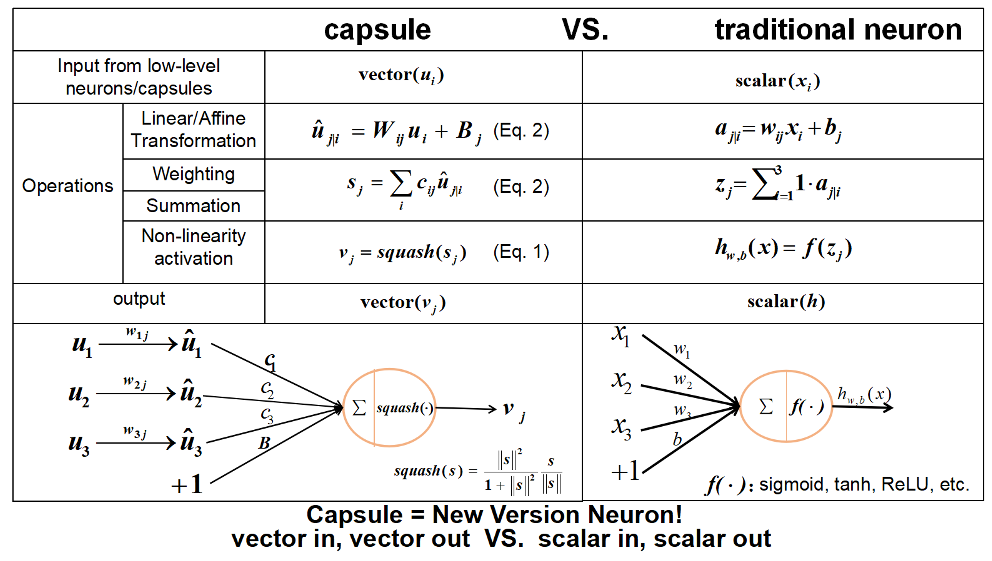（图源：Github-CapsNet-Tensorflow-README）
2.2.2 动态路由机制
动态路由机制主要决定上层$Capsule$主要由哪几个下层$Capsule$组成，具体步骤如下：
- 初始化第$l$层所有$Capsule$与第$l+1$层的$Capsule_j$所有耦合系数为0
- 归一化所有耦合系数，并对第$l$层所有$Capsule$的预测向量进行加权求和，然后对结果进行非线性压缩（本步骤就是指上一节中详细描述的计算过程）
- 借助上一步得到的$Capsule_j$输出向量$v_j$，对耦合系数$b_{ij}$进行更新：$$b_{ij}\leftarrow b_{ij}+\hat u_{j|i}\cdot v_j$$
- 步骤2和步骤3重复$r$次，完成耦合系数的更新（在本文后续实验中$r=3$）
具体算法伪代码如下：
更新的本质：向量$\hat u_{j|i}$是$Capsule_i$的输出向量$u_i$经权重矩阵$W_{ij}$仿射变换得到的，向量$v_j$是$Capsule_j$的输出向量，所以$\hat u_{j|i}\cdot v_j$描述的是$Capsule_i$的输出与$Capsule_j$的输出的一致性（agreement），具备一致性的底层特征将共同组成高级特征。
两层Capsule间的动态路由机制与K-means聚类算法存在惊人的一致性，对比来说，如果把底层特征看作样本，高级特征看作簇心，底层特征组成为高级特征相当于一个无监督的聚类分组的过程，也是一个在神经网络网状结构内部构建树结构的过程。
2.2.3 构建CapsNet网络
首先构建一个三层的简单$CapsNet$网络，第一层是普通卷积层，第二层是主胶囊层（$PrimaryCaps$），第三层是数字胶囊层（$DigitCaps$），图示如下：
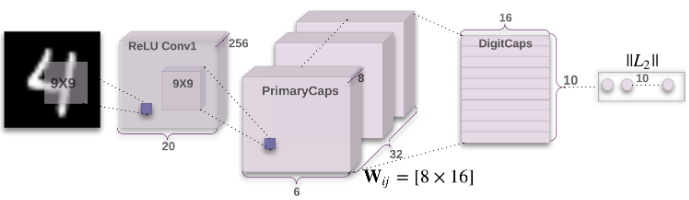
普通卷积层的输入为$28\times 28$的手写数字图片，本层包含$256$个$9\times 9$的卷积核，步长为$1$，使用$ReLU$作为激活函数，最终普通卷积层的输出维度为$20\times 20 \times 256$（补充说明：$20=28-9+1$），参数量为$(9\times 9 +1)\times 256=20992$
主胶囊层其实是一个卷积胶囊层，共包含$32$个胶囊，每个胶囊包含$8$个$9\times 9\times 256$的卷积核，步长为$2$，使用$Squashing$作为激活函数，最终主胶囊层的输出维度为$32\times 8 \times 6 \times 6$（补充说明：$6=\frac{20-9+1}{2}$），参数量为$32\times 8 \times (9\times 9 \times 256 + 1)=5308672$
数字胶囊层共包含$10$个胶囊，对应数字的$10$种类别。每个胶囊是由上一层的胶囊输出通过动态路由的方式计算得到的，而上一层胶囊共计产生了$6\times 6 \times 32=1152$个向量，每个向量维度为$8$，这些向量在数字胶囊中通过一个$8\times 16$的权重矩阵转为$16$维向量，也就是说数字胶囊层的输出维度为$16\times 10$，参数量为$1152\times (8\times 16 + 2)=1497600$，其中$8\times 16$为权重矩阵的参数，$2$表示耦合系数和标准化后的耦合系数
2.2.4 边缘损失函数
由上文可知，$Capsule$是对实体的实例参数化，$Capsule$的输出向量的模长表示实体存在的概率，所以一个理想的$Capsules$网络其最顶层的$DigitCaps$输出向量模长应尽可能明显，而这一点可以通过设定边缘损失函数实现约束与引导，对于$Capsule_k$其对应的边缘损失函数为： $$L_k=T_k max(0,m^+-||v_k||^2)+\lambda(1-T_k)max(0,||v_k||-m^-)$$
- 其中$T_k$表示分类类别（比如MINIST就是10中数字类型），为布尔型变量
- 边缘损失根据最顶层$DigitCaps$是否归属于类别$T_k$划分为两项
- 前一项对输出向量模长最大值进行约束，其中$m^+$表示上边界，本文设为$0.9$
- 前一项对输出向量模长最小值进行约束，其中$m^-$表示下边界，本文设为$0.1$
- 超参数$\lambda$用于权衡上边界约束与下边界约束，一般更重视前者，所以设$\lambda=0.5$
最终模型的损失函数是最顶层所有$Capsule$边缘损失的总和
2.2.5 添加解码模块
根据Capsules与自编码器变体可知，借助自编码器的形式，$Capsules$网络能更快的实现对实体的实例参数化，所以本文也沿用了这一特性。具体来说，对于$DigitCaps$层的向量输出，本文添加了由三个全连接层构成的解码器，用于还原图像，图示如下：
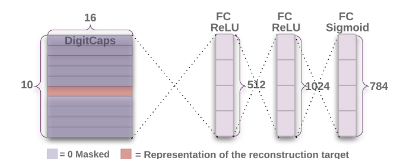
对于每个类别，解码器会掩盖（mask）掉不相干的$Capsule$，仅保留与类别相关的$Capsule$用于解码，三个全连接层的输出维度分别为$512,1024,784$，对应的激活函数分别为$ReLU, ReLU, Sigmoid$，最后一层的$784$神经元输出会还原为$28\times 28$的图像
实际使用中，解码器反馈的损失误差通过乘以$0.0005$的方式进行压缩，以保障边缘损失的主导地位，同时也借助解码器加速$Capsule$构建实例化参数的过程
2.3 实验与评价
本实验采用$Tensorflow$框架，优化器使用$Adam$
选择$MINIST$数据集中的$6$万图片进行训练，$1$万图片进行预测
解码器效果展示：
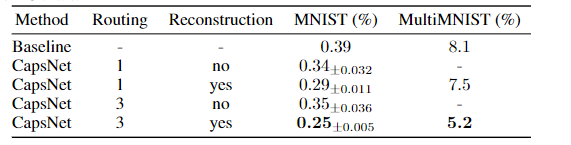
不同动态路由次数、是否添加解码模块的对比（Baseline是普通三层CNN）：
对于$DigitCaps$的最终$16$维输出进行随机扰动，扰动范围为$[-25%,25%]$，扰动间隔为$5%$，并通过解码器进行结果的可视化：
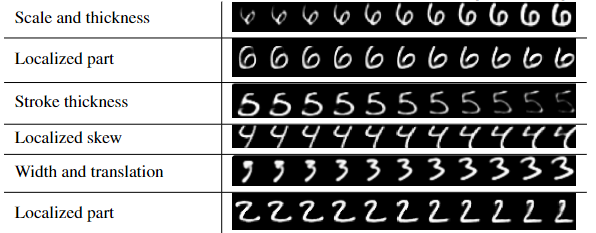
可以发现$DigitCaps$的每个维度都学到了类似于放缩、粗细、旋转、具备变形等概念
鲁棒性测试：对测试集添加随机小范围仿射变换，普通$CNN$的准确度由$99.22%$降到了$66%$，而$Capsules$网络的准确度从$99.23%$降到了$79%$
$MultiMNIST$是通过叠加$MINIST$数据集中的图片得到的数据集，而本文中的$Capsule$模型的最终错误率仅为$5%$，效果展示如下：
总结：
- 胶囊网络一定程度上学到了实体部分与整体之间的空间关系，具备视角不变性，从而取得了出色的模型稳健性和泛化能力。
- 胶囊使用向量表示实体的实例化参数，还能利用矩阵乘法有效建模空间关系。
- 类似于生成式网络，过于关注于全局信息，面对图片背景复杂的场景略显吃力
- 胶囊非常擅长处理图像分割的问题，展现出来巨大的探索潜力
3 Capsule后记
Capsules扩展阅读：
Capsules后续发展：
Matrix Capsules with EM Routing (2018)：Capsule的输出由向量扩展为矩阵+标量（矩阵描述分布，标量描述概率/熵）；动态路由部分从简版K-means聚类转变为简版GMM聚类（无监督分类问题转为概率分布描述问题）实现了Capsul版的卷积（局部版的动态路由）
Stacked Capsule AutoEncoder (2019)：使用无监督的方式达到了98.5%的MNIST分类准确率
Capsules领域融合：