个人笔记

前置知识：贝叶斯算法、高斯过程回归

BNN 的定义

贝叶斯神经网络（Bayesian neural networks, BNNs）：

• 神经网络中的可训练参数，即权重（weight）和偏置（bias）都表示为一个分布
• 一种最简单的 BNN 就是将模型参数看作服从均值为 $\mu$，方差为 $\delta$ 的高斯分布；考虑到中心极限定理的存在，一般认为模型参数符合高斯分布是一种合理的假设
• 在预测时，BNN 会从每个高斯分布采样，得到一个确定的神经网络，然后用于预测；也可以对参数多次采样后分别进行预测，然后将多次预测结果进行汇总（类

Read more

循环神经网络（RNNs）：具有隐状态、不同层参数共享的神经网络

常见的三种基础 RNNs ：RNN、GRU、LSTM

RNN

隐变量模型：使用隐状态 $h_{t-1}$ 存储前 $t-1$ 步的序列信息 $$P(x_t|x_{t-1},...,x_1)\approx P(x_t|h_{t-1})$$ $$h_t=f(x_t,h_{t-1})$$ 循环神经网络（recurrent neural networks，RNNs） 是具有隐状态的神经网络

假设时刻 $t$ 的输入为 $X_t \in \mathbb{R}^{n\times d}$，对应的权重参数为 $W

Read more

卷积神经网络（CNN）：引入了卷积操作的神经网络

普通卷积

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation）

二维互相关运算示例：

汇聚/池化层

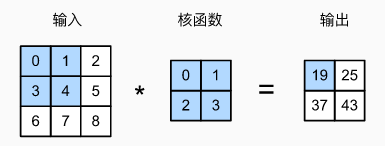
池化（pool）层的优点：降低卷积层对位置的敏感性

常用池化层分两种：最大池化层和平均池化层，前者示例如下：

类似于卷积层，池化层也会有填充和步幅，使用大于 1 的步幅可以起到降维的作用

不同于卷积层，池化层在每个输入通道上是单独计算的，所以池化层的输出通道数等于输入通道数

膨胀卷积

膨胀（dilated）卷积，也称

Read more

一个典型的神经元

• Axon 轴突
• Dendritic tress 树突
• Axon hillock 轴突体

线性神经元

$$y = b+\sum_ix_iw_i$$

二进制阈值神经元

对线性加权运算的结果，进行阈值判定

$$z = b+\sum_ix_iw_i$$ $$\begin{equation} y = \left\{ \begin{array}{rl} 1 & \mbox{if } z \geq 0, \\ 0 &

Read more

1 word2vec概述

广义上指能将词语文本转化为向量的一类技术，也称词嵌入（word embedding）

狭义上指借助神经网络模型为基础构建词向量的过程，其中最经典的两类word2vec技术分别为skip-gram和CBOW

最终获取的词向量，可看作表示单词意义的向量，也可以看作是词的特征向量

2 word

Read more