分类目录归档：迭代优化算法
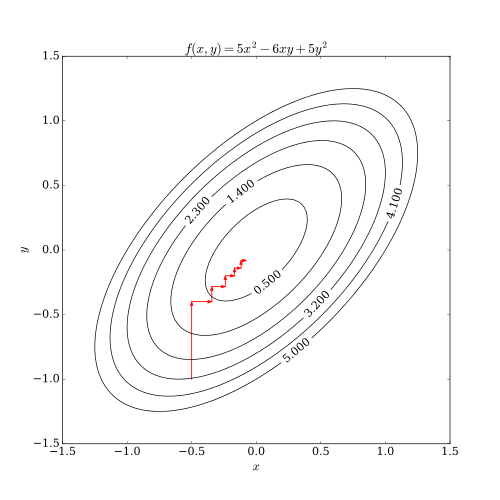
首先，理解梯度向量是指向函数值增长最快的方向的：MIT18.02笔记-梯度的定义与理解
定义函数$f(x)$，其在点$x$处沿着方向$d$的变化率可用方向导数表示，即梯度与方向的乘积： $$Df(x;d)=\nabla f(x)^Td$$ 当$d=-\frac{\nabla f(x) }{ ||\nabla f(x)|| }$时，函数$f$在点$x$处的下降速率最大，即负梯度方向为最速下降方向
最速下降算法：在迭代过程，每次都选择负梯度方向搜索（对于寻找最小值的最优化问题）
最速下降算法步骤：
贝叶斯优化是一种通用的黑盒优化算法，不需要计算梯度便可快速解决最优化问题，贝叶斯优化适合处理目标函数计算成本高或求导困难的情况。贝叶斯优化最常用的场景是超参搜索（尤其是神经网络类算法，计算成本高，超参数还多）
贝叶斯优化(Bayesian Optimization，BO)
目的是要找到一组最优的超参组合x，能使评价/目标函数f(x)达到全局最优
由于评价/目标函数f(x)计算成
在最优化问题的求解过程中常利用到函数梯度及其高阶信息
牛顿法（Newton's method）又称为牛顿-拉弗森方法（Newton-Raphson method）
牛顿法借助泰勒级数的低阶展开，寻找方程$f(x)=0$的根（因此也被称为切线法）
牛顿法计算步骤：
期望最大化（Expectation-Maximum，简称EM）算法是一种机器学习常见基础算法
EM算法常用于处理存在隐变量的最大似然估计模型，训练过程简单描述如下：
以K-means聚类为例进行直观理解：
EM算法作为一种基础算法，广泛应用于多种算法模型的学习过程，比如：[[1_study/algorithm/概率图类模型/隐马尔可
大部分机器学习模型的构建都是寻找最小损失函数的过程，而梯度下降法（Gradient Descent）便是一种常见迭代优化算法，用于寻找损失最小的参数解。
以简单二次函数为例进行算法的简单说明，模型形式
坐标下降法（英语：coordinate descent）是一种非梯度优化算法。算法在每次迭代中，在当前点处沿一个坐标方向进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。对于不可拆分的函数而言，算法可能无法在较小的迭代步数中求得最优解。
为了加速收敛，可以采用一个适当的坐标系，例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系，即自适应坐标下降法。
在统计学中，最小角回归(LARS)是一种将线性回归模型拟合到高维数据的算法
用 $T(\hat{\boldsymbol{\beta}})$ 表示 $\hat{\boldsymbol{\beta}}$ 的绝对值范数 $$T(\hat{\boldsymbol{\beta}})=\sum_{j=1}^m|\hat{\beta_j}|\tag{7}$$ 则Lasso即为下面的约束优化问题： $$\min S(\hat{\boldsymbol{\beta}}) \quad \text{s.t.} \quad T(\hat{\boldsymbol{\beta}}) \le t\tag{8}$$ Las