分类目录归档：algorithm
将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置
2D几何变换分类：
主成分分析（Principal components analysis，PCA），一种常用的线性降维方法
算法步骤：
图像理解：
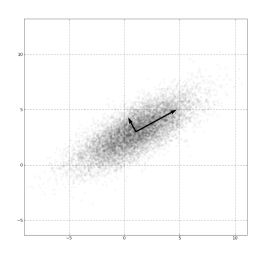（图源：维基百科-主成分分析）
PCA 的优缺点分析：
尺度不变特征变换匹配算法（Scale Invariant Feature Transform 简称 SIFT）
SIFT算法常用来提取用于描述影像中的局部性特征，算法主要从空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量
算法过程：
期望最大化（Expectation-Maximum，简称EM）算法是一种机器学习常见基础算法
EM算法常用于处理存在隐变量的最大似然估计模型，训练过程简单描述如下：
以K-means聚类为例进行直观理解：
EM算法作为一种基础算法，广泛应用于多种算法模型的学习过程，比如：隐马尔可夫模型 HMM
这类算法思想在其他模型中也经常遇见，比
Chinese Whispers（简称CW）算法，是一种无监督的图聚类算法
CW算法运行效率高，但结果存在不确定性，常用于人脸聚类或文本聚类
以人脸聚类为例，先进行图的初始化（构建无向加权图）：每个人脸图片为一个节点，不同节点通过计算相似度，然后连接相似度超出指定阈值的节点，并以相似度作为边的权重
算法步骤
- 对于N个人脸样本，每个样本节点先单独成簇（自成一类）
- 遍历所有节点，根据每个节点的邻节点所属类别，计算权重累加
- 修正节点类别，选择最终累加权重最高的类别
- 如果有多个权重最高的类别，
K均值算法（即，k-means clustering），是一种无监督聚类算法
K-means算法属于NP-hard问题，不过存在高效的启发式算法，能快速收敛到一个局部最优解
算法步骤
- 对于N个样本，随机选择其中K个，作为最初的质心
- 遍历所有样本，选择最新的质心进行归类，形成K个簇
- 根据每个簇的样本重新计算质心（比如求均值）
- 重复步骤2-3，直到每个簇质心基本不再变化或达到最大迭代次数
算法的收敛过程如下所示：
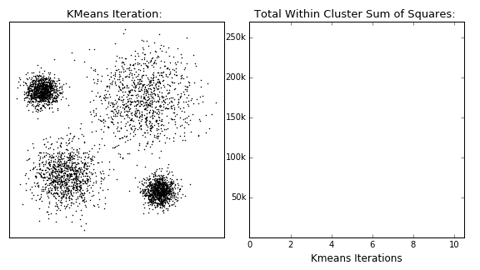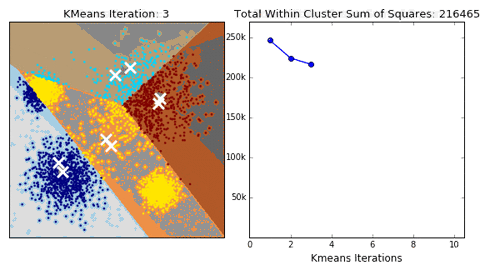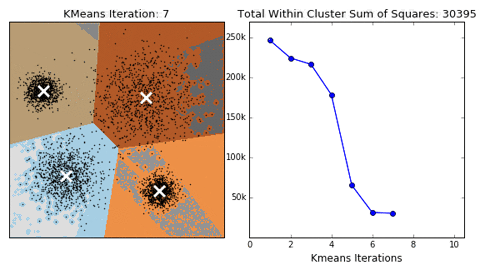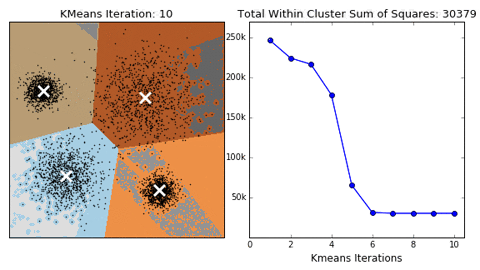（图源来自https
一个无向图，结点表示随机变量，边表示两个随机变量之间的概率依赖关系，每个随机变量都可以指定一种可能取值，当变量满足马尔可夫性（即变量的可能取值只与它的临近变量有关）时，这时的图就叫马尔可夫网络，也就是马尔可夫随机场。（非严谨定义）
以构建以词性标注为例，假设一个句子由10个单词组成的句子，每个单词的词性选择有10种，则马尔可夫随机场就限制了所有单词的词性只和它前后的单词有关系。
条件随机场
前置知识：1_study/math/马尔可夫模型
可视马尔可夫模型的状态是可知的，而隐马尔可夫模型（The Hidden Markov Model，简称 HMM）的状态是不可知，但存在可知的序列观察值
以典型的看病模型为例，设病人的状态有两种：{健康（Healthy），发烧（Fever）}
医生不能直接知道病人的状态，但能够得知病人的健康状况：{正常（Normal），发寒（Cold）， 头晕（Dizzy）}，作为一个行医多年的鬼才医生，他可以构建出看病用的隐马尔可夫模型：
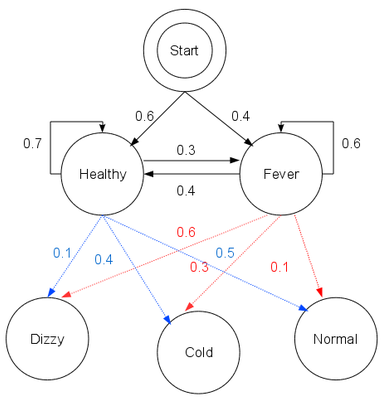
注
概率图模型，在概率模型的基础上，使用基于图的方法来表示概率分布（概率密度/密度函数），是一种通用化的不确定性知识表示和处理方法。
在图模型中，随机变量构成了图中的节点，而随机变量之间的关系（比如相关、独立、不独立、条件独立、因果）则构成了图中节点之间的边
随机变量的常见关系度量指标：
对于随机变量之间的因果关系分析
（图源：维基百科-自编码器）