1 基本信息

英国作家和电影制作人,内容创意制作者和网络搞怪小能手
2 个人经历
2.1 达利奇小屋
在兼职水军帮餐厅写好评的过程中,乌巴·巴特勒发现,一个精选好评只价值10英镑
面对着越来越多的虚假好评,餐厅的生意会越来越好,而味道反倒变得不再那么重要
由此乌巴·巴特勒产生了一个大胆的想法,就是构建一个《不存在的网红餐厅》
具体操作过程:
- 购买一处偏远的房屋,配备上最简单的设备
- 在猫途鹰网站注册餐厅,起名为“达利奇小屋”
- 为餐厅打造官网,伪造诱人

英国作家和电影制作人,内容创意制作者和网络搞怪小能手
在兼职水军帮餐厅写好评的过程中,乌巴·巴特勒发现,一个精选好评只价值10英镑
面对着越来越多的虚假好评,餐厅的生意会越来越好,而味道反倒变得不再那么重要
由此乌巴·巴特勒产生了一个大胆的想法,就是构建一个《不存在的网红餐厅》
具体操作过程:
皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称PPMCC或PCCs)
目标:在Ubuntu 18.04配置CUDA 11.3 和 cuDNN 8.8.0
环境说明:容器内已配置显卡驱动+torch-gpu版
nvcc -Vnvidia-smirunfile(local)版本后,官网会直接给出了安装指令wget https://developer.download.nvidia.com/compute/cuda/11.3.0/local_installers/cuda_11.3.0_465.19.01_给定均值向量和协方差矩阵,可以唯一确定一个高斯分布(Gaussian distribution)
给定均值函数和协方差函数,可以唯一确定一个高斯过程(Gaussian Process,GP)
假设自变量为时间$t$,则每一个时刻$t$,高斯过程都对应着一个高斯分布
当时间$t$是连续型变量时,整个高斯过程便对应着无数个高斯分布,所以高斯过程可看作无限维高斯分布
高斯分布的两
ASCII(American Standard Code for Information Interchange),也称 ANSI
A 对应的二进制数值是 01000001,对应的十进制就是65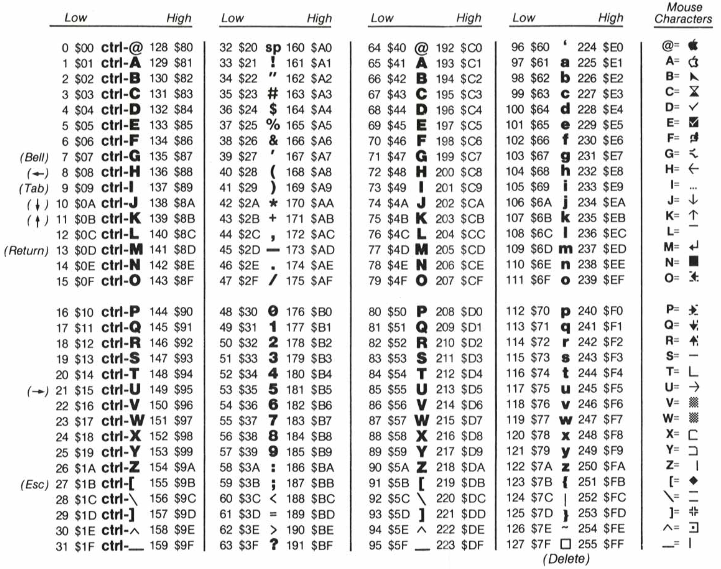
EASCII ,在 ASCII 基础上的扩展(由原来的 7 位扩充到 8 位),它完全兼容 ASCII,额外包括表格符号、计算符号、希腊字母和特殊拉丁符号
GB2312 编码,又称 GB0,1981由中国国
https://www.latexlive.com/home :支持快捷工具、公式模板、公式图片识别
国产收费公式&数据图工具: https://www.amyxun.com/
A
实现步骤:
class=internal-linktouchend,mouseenter或mouseleave事件mouseenter事件时,访问超PyCaret是一个开源的、低代码的Python机器学习库,可以实现机器学习工作流程的自动化。作为一个端到端的机器学习和模型管理工具,PyCaret可以成倍地缩短实验周期,实现更有效率的科研探索。
TableOne是一个很简单实用的小工具,能对数据进行基本统计展示
基本特性:
使用注意事项:
categorical显式指定