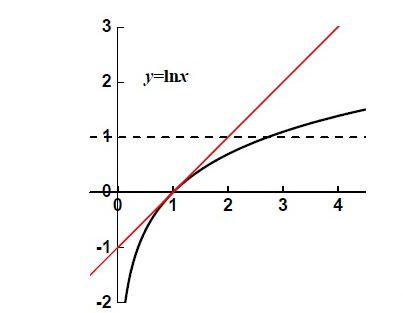
1 对数的定义与性质
definition of the logarithm: $$L(x)=\int_1^x\frac{1}{t}dt$$
对数函数的性质
- $L'(x)=\frac{1}{x}$与$L(1)=\int_1^1\frac{1}{t}dt=0$,这两个性质唯一的确定对数函数
- 由$L''(x)=-\frac{1}{x^2}$可知,函数处处下凹
- $L'(1)=1$,函数图像在点$(1,0)$位置与$y=x-1$相切
- 函数图像与$y=1$相交于点$(e,1)$,即$e$满足$L(e)=1$
证明:$L(ab)=L(a)+L(b)$
- $L(ab)=\int_1^a\frac{1}{t}dt+\int_a^{ab}\frac{1}{t}dt=L(a)+\int_a^{ab}\frac{1}{t}dt$
- 采用换元法,令$t=au$,则$dt=adu$
- $\int_a^{ab}\frac{1}{t}dt=\int_1^{b}\frac{1}{u}du=L(b)$
- 积分上下限一般情况下是不可约的,此处换元法只是几何上的伸缩
- 对数函数的上下限是可约的,例如$ln4-ln2=ln2-ln1$
2 几种特殊的定积分函数
误差函数(short-for-error function,简称erf) $$erf(x)=\frac{2}{\sqrt{\pi}}\int_0^xe^{-t^2}dt$$
- 此函数在上一节微积分基本定理的应用有提及
- 它是一个钟型函数,并且拥有两条渐近线: $lim_{x\to \infty}F(x)=\frac{\sqrt{\pi}}{2}$ 和 $lim_{x\to -\infty}F(x)=-\frac{\sqrt{\pi}}{2}$
- 误差函数正是数学家为了将函数值极限变为1,拼凑出来的一个函数
- 误差函数的另一种变体是标准正态分布$f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2}dx$
菲涅尔积分(Fresnel integral) $$C(x)=\int_0^xcos(t^2)dt$$ $$S(x)=\int_0^xsin(t^2)dt$$
傅里叶分析中常用的函数 $$H(x)=\int_0^x\frac{sint}{t}dt$$
黎曼假设:小于$x$的素数个数约等于 $$Li(x)=\int_2^x\frac{1}{lnt}dt$$
3 定积分的几何应用
定积分表示在某个区间上函数曲线与$x$轴所围成的面积
所以可以用于求解多个函数曲线所围成图像的面积,具体过程略
4 参考