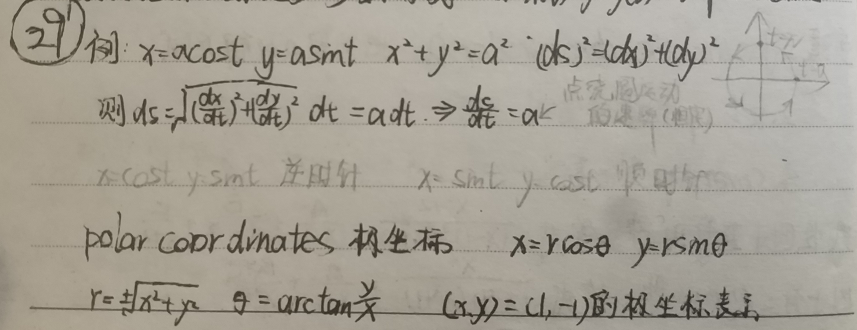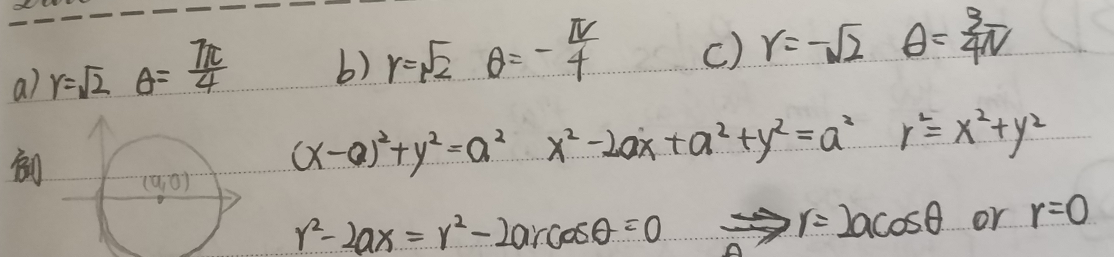1 参数方程示例
$$x=acost,y=asint$$
- 一个明显性质是$x^2+y^2=a^2$,极限状态下$(ds)^2=(dx)^2+(dy)^2$
- 则$ds=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt=adt$
- 也就是$a=\frac{ds}{dt}$,$a$描述的是一种恒定速率
- 此参数方程描述的是一种逆时针匀速圆周运动,其中圆的半径为$a$
- 当$x=sint,y=cost$时,参数方程描述的是一种顺时针匀速圆周运动
2 极坐标 polar coordinates
极坐标是对二维平面上点的另一种坐标描述(距离$r$与夹角$\theta$)
$$(x,y)\to x=rcos\theta,y=rsin\theta$$ $$r=\pm \sqrt{x^2+y^2},\theta=arctan\frac{x}{y}$$
示例1:坐标$(x,y)=(1,-1)$的三种极坐标表示形式
- $r=\sqrt{2},\theta=\frac{7\pi}{4}$
- $r=\sqrt{2},\theta=-\frac{\pi}{4}$
- $r=-\sqrt{2},\theta=\frac{3\pi}{4}$
示例2:圆心在$(a,0)$并且半径为$a$的圆
- 由原始方程$(x-a)^2+y^2=a^2$可得$x^2-2ax+a^2+y^2=a^2$
- 带入$r^2=x^2+y^22$可得$r^2-2ax=r^2-2arcos\theta=0$
- 化简可得$r=2acos\theta\ or \ r=0$
3 参考