在最优化问题的求解过程中常利用到函数梯度及其高阶信息
- 这类算法最常见的就是梯度下降法和牛顿迭代法
- 梯度下降考虑了函数的一阶导数, 是一种一阶优化方法
- 牛顿算法考虑了函数的二阶偏导, 是一种二阶优化方法
1 牛顿迭代法
牛顿法(Newton's method)又称为牛顿-拉弗森方法(Newton-Raphson method)
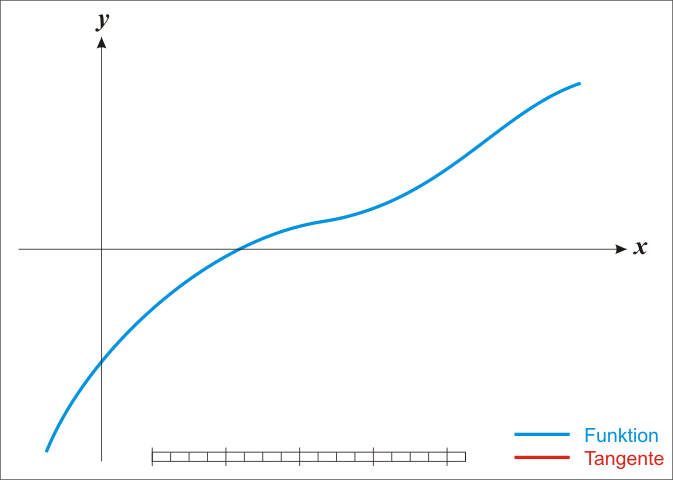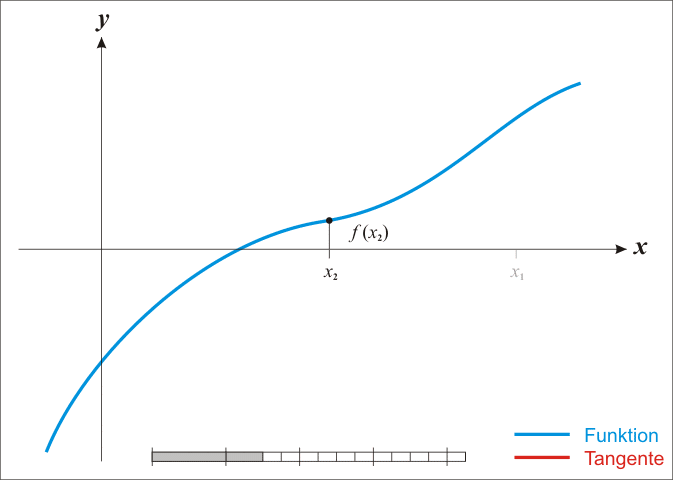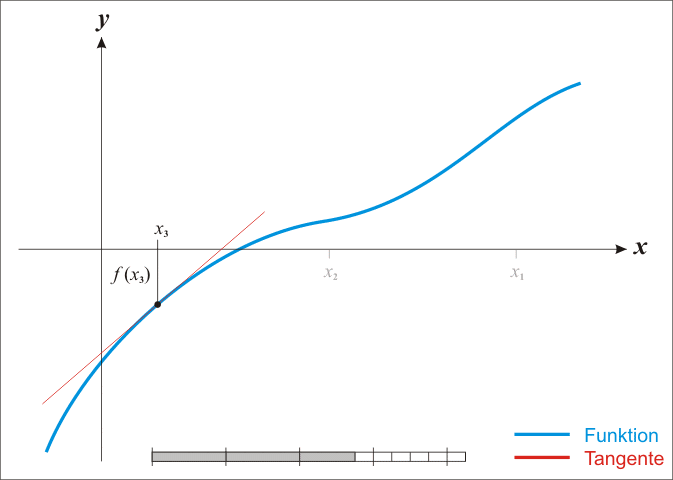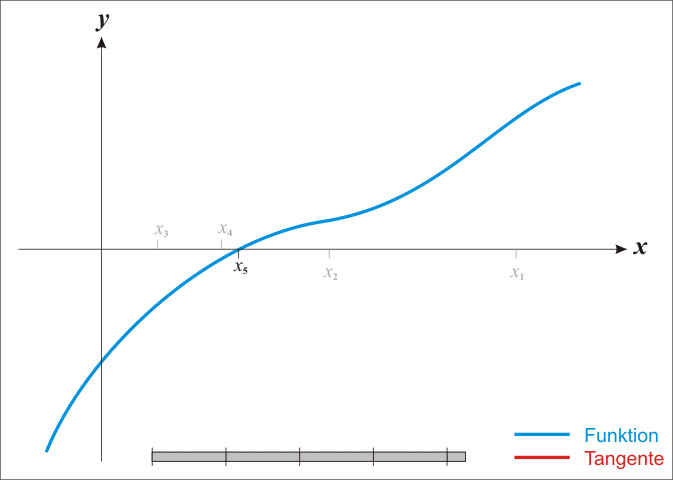
牛顿法借助泰勒级数的低阶展开,寻找方程$f(x)=0$的根(因此也被称为切线法)
牛顿法计算步骤:
- 随机初始化$x=x_0$,尽量选择靠近方程根的位置
- 仅考虑泰勒级数的一阶展开,构建过点$(x_0,f(x_0))$且斜率为$f'(x_0)$的直线
- 寻找直线与$x$轴交点,将交点的$x$坐标记为$x_1$
- 重复以上过程$n$次,其中第$n$次的迭代公式为$x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)}$
- 当迭代次数达到指定最大值,或$\Delta x$几乎不变化时,停止迭代
- 此时得到的$x_{final}$即为方程$f(x)=0$的近似根
图示如下:
1.1 收敛性分析
假设迭代到第$k$次时,$x$的取值为$x_k$,与最优值的距离为$e_k=x_k-x_{opt}$
由此可得以下公式: $$f(x_{opt})=f(x_k-e_k)=0$$ 借助泰勒展开对上式进行简化,可得结果: $$f(x_k)-e_kf'(x_k)+\frac{1}{2}e_k^2f''(\xi_k)=0$$ 其中$\xi_k$的取值在$[x_k-e_k,x_k]$之间
考虑牛顿法的迭代公式$x_{k+1}=x_{k}-\frac{f(x_k)}{f'(x_k)}$,所以: $$e_{k+1}=e_k-\frac{f(x_k)}{f'(x_k)}=e_k-\frac{e_kf'(x_k)-\frac{1}{2}e_k^2f''(\xi_k)}{f'(x_k)}=\frac{1}{2}e_k^2\frac{f''(\xi_k)}{f'(x_k)}$$ 当$|\frac{f''(\xi_k)}{f'(x_k)}|<c$时,易得$e_{k+1}\leq ce_k^2$
由此可知,误差随着迭代次数呈现二次递减的趋势;初始$e_0$越小,算法的收敛速度越快;对于$f'(x_k)$接近0的位置,算法的收敛速度会受到很大影响
1.2 优缺点分析
牛顿迭代法优点:
- 复杂方程的求导过程困难,很适合使用牛顿法计算近似根
- 牛顿迭代法收敛速度快,虽然求出的是近似根,但一般精度较高
- 当函数$f(x)$表示$F(x)$的导函数时,可用于求解$F(x)$的最优化问题
牛顿迭代法缺点:
- 不适合求导困难的函数,初始值的选择需要尽量靠近最优解
- 牛顿迭代法无法处理重复根,并且可能收敛到局部最优解
- 当斜率接近0或处于拐点位置时,牛顿迭代法也容易出现问题
2 拟牛顿类算法
牛顿类算法通过求导(在矩阵运算中就是求解Hessian矩阵)确定搜索方向。但在大规模问题中,计算Hessian矩阵以及逆矩阵的代价过高,因此诞生了一批拟牛顿类算法(Quasi Newton Algorithm)
拟牛顿类算法在每次迭代过程中,以较小的计算代价生成近似Hessian矩阵或其逆矩阵,因此这类算法也被称为Hessian-Free Optimization。BFGS是一种最常见的拟牛顿类算法
2.1 BFGS算法
BFGS算法, 以其发明者Broyden, Fletcher, Goldfarb和Shanno命名
BFGS算法伪代码:

- 使用$B_k$来逐步逼近Hessian矩阵$H_k$
- Hessian矩阵的大小为$O(N^2)$, 其中N为参数的个数
- 当初始$B_0$为正定矩阵时,迭代中的$B_k$也会是正定矩阵
2.2 其他拟牛顿类算法
[[1_study/algorithm/迭代优化算法/共轭梯度法]]
L-BFGS 算法:有限内存版的BFGS(只保存最近的m次迭代信息),适用于内存不足的情况
OWL-QN 算法:L-BFGS算法的变体,增加了L1正则项,使用次梯度决定搜索方向
Broyden's method:优化了牛顿法的雅可比矩阵的计算(变成迭代式更新)
DFP 算法:在高维矩阵中,通过正割法找到最接近当前估计并满足曲率条件的方程解
(精力有限,有缘再研究)