蒙特卡洛法
发表评论
1678 views

蒙特卡洛法 MC

蒙特卡洛方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。

蒙特卡洛方法的名字来源于摩纳哥的一个城市蒙特卡洛，该城市以赌博业闻名，而蒙特卡洛方法正是以概率为基础的方法。与它对应的是确定性算法。

蒙特卡洛方法的原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬

蒙特卡洛方法举例

以一个经典的题目《计算圆周率》来说明：

核心思路：

  • 构建一个边为2的正方形，使其中心作为坐标原点
  • 构建一个半径为1的圆形，使其圆心位于坐标原点
  • 在正方形内随机取点，统计点落在圆形的次数
  • 随着统计次数的增加，点落在圆形的概率逼近二者面积比
  • 根据正方形面积与面积比反推圆的面积，最终得出圆周率$\pi$

代码实现：

import random
import time
count,total_count = 0,10**6
start = time.perf_counter()
for i in range(0, total_count):
    x = random.uniform(-1,1)
    y = random.uniform(-1,1)
    if (x*x + y*y)**(1/2) < 1: # 判断随机生成的点是否在圆内
        count=count+1
pi = 4*count/total_count # pi=正方形面积*（在圆内的次数/总次数）
print("pi = {:.5f}".format(pi))
# pi = 3.14256

拟蒙特卡洛方法(Quasi-Monte Carlo method)是使用低差异列（一种确定生成的超均匀分布列，也称为拟随机列、次随机列）来进行数值积分和其它数值问题的研究； 而普通的蒙特卡洛方法使用的是伪随机数

蒙特卡洛树搜索 MCTS

蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）

  • 一种基于树结构的蒙特卡洛方法，可以根据确定的规则进行启发式随机搜索
  • 树结构形成了一个可行解的解空间，其大小为$2^N$（$N$等于决策次数，即树深度）
  • MCTS还需要一个可量化的损失函数，用于评估解的优劣
  • 在计算完一条路径的损失成本后，MCTS会通过反向传播更新此路径上的节点
  • MCTS算法会遵循损失最小化的原则在整个搜索空间上进行启发式搜索，直到找到一组最优解或达到最大迭代次数

MCTS的核心特点：在确定方向的渐进收敛（树搜索的准确性）和随机性（随机模拟的一般性）之间寻求一个最佳平衡

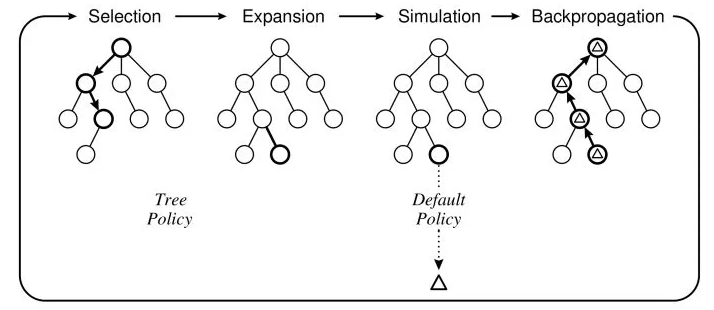
MCTS的搜索就是建立一棵树的过程

  • 初始化：此时搜索树只有一个根节点
  • 搜索树的所有节点都会包含三个基本信息：1.下一步可选的动作 2.该节点被访问的次数 3.该节点的累计评分（用于提供一个确定性的收敛方向）
  • 树的拓展：在可选的动作中随机选择一个，并根据动作的结果/状态，创建一个子节点；针对每个新建立的子节点进行一次完整的随机模拟，将最终的结局（胜1负0）作为该节点的初始评分
  • 树的搜索：当所有可选动作均已被拓展过时，表明该节点已经完成一个完整搜索（complete search），此时依次计算所有子节点的UCB值，并选择UCB值最大的子节点
  • 在MCTS算法执行中，树会优先考虑拓展操作，其次才是搜索操作
  • 反向传播：每一次的模拟过程都对应着树中的一条路径，抵达终点时，需要根据终点结果对路径上的所有节点进行累积评分的更新
  • 随着迭代次数的增加，搜索树的规模会不断扩大，对应的累积评分也将更加合理

算法细节1：UCB值的计算公式 $$UCB=v_i+C\times \sqrt{\frac{lnN}{n_i}}$$

  • 其中$v_i$表示节点$i$的累计评分，$n_i$表示节点$i$被访问的次数
  • $N$表示其父节点被访问的总次数，$C$为可调整的超参数（常取值为2）
  • 当$n_i=0$时，UCB值公式的右侧趋近于无穷大，因此树搜索会优先选择未探索过的节点；UCB值公式的左侧则会约束搜索尽可能前往累计评分高的解空间

算法细节2：累计评分的更新方法没有标准方法，最简单的更新方式就是当一次模拟过程的结果是胜利时，则对应路径的所有节点的累计评分+1

算法细节3：当搜索空间过大时（如围棋），MCTS会有选择地朝某些方向进行深度搜索，同时选择性地放弃一些显然不合理的方向（比如以某一节点展开多次随机模拟后，发现每次都是输，那就可以考虑放弃该节点的后续探索）

蒙特卡洛树搜索的典型应用：AlphaGo Zero：无师自通的围棋大师

马尔可夫链蒙特卡洛 MCMC

前置知识：1_study/math/马尔可夫模型

马尔可夫链蒙特卡洛法 (Markov Chain Monte Carlo, MCMC)

  • 一种基于随机游走的从复杂概率分布中进行采样的蒙特卡洛方法
  • 假设马尔可夫链的状态转移矩阵为 $Q$，其对应的平稳分布为 $\pi(x)$
  • 但是使用 MCMC 的前提是马尔可夫链满足细致平稳条件，即：

$$ \pi(i)Q(i,j) \neq \pi(j)Q(j,i) $$

细致平稳条件确保了马尔可夫链的收敛性质，即状态转移矩阵存在平稳分布

现实中的马尔可夫链很难满足细致平稳条件，因此需要引入 $\alpha(i,j)$ 来改造上式 $$ \pi(i)Q(i,j)\alpha(i,j) = \pi(j)Q(j,i)\alpha(j,i) $$

  • 其中 $\alpha(i,j) = \pi(j)Q(j,i)$，$\alpha(j,i) = \pi(i)Q(i,j)$
  • 改造后的状态转移矩阵 $P$ 可表示为：$P(i,j) = Q(i,j)\alpha(i,j)$
  • $\alpha(i,j)$ 一般称之为接受率，取值在 $[0,1]$ 之间
  • 矩阵 $Q$ 通过一定的接受-拒绝概率，改造得到新矩阵 $P$

MCMC 的采样过程：

  1. 对于时刻 $t$ 对应的状态 $x_{t}$，根据条件概率分布 $Q(x|x_{t})$ 采样得到 $x_{*}$
  2. 从均匀分布中采样 $u \sim uniform[0,1]$，并进行接受-拒绝的概率判定
  3. 如果 $u < \alpha(x_t,x_{*}) = \pi(x_{*})Q(x_{*},x_t)$，则接受转移，即 $x_{t+1}=x_{*}$
  4. 否则不接受转移，即 $x_{t+1}=x_{t}$
  5. 重复以上过程，直到获取到充分的采样样本

MCMC 采样优化：Metropolis-Hastings 采样，简称 M-H 采样

  • 该方法是对 MCMC 采样的效率改进，避免了 MCMC 接受率过低的问题
  • 其核心变动在于，在满足细致平稳条件下调整了 $\alpha(i,j)$ 的定义：

$$\alpha(i,j) = min{ \frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1}$$

Gibbs 采样：M-H 采样的高维度版本，每次随机选择一个坐标轴进行采样

参考

蒙特卡罗方法、蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）初探

往年同期文章