元学习
- 一种因果效应评估的学习范式,属于潜在结果框架
- 需要根据实际的业务场景来选择不同类型的元学习方法
- 元学习的效果也高度依赖所选择和组合的机器学习方法
S-Learner
S 学习器(S-Learner)是一种最简单的元学习方法
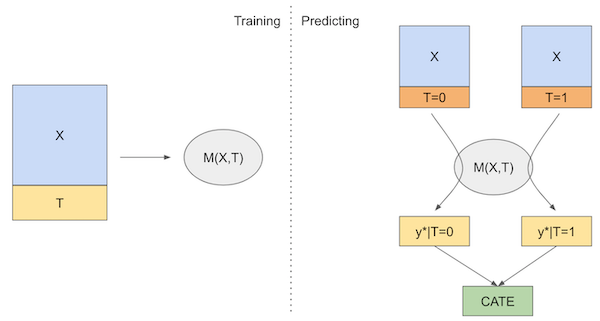
- 先训练模型 $M_{s}$ 来根据外生变量 $X$ 和干预变量 $T$ 来预测结果
- 之后在推理阶段,通过指定不同的干预变量取值,来推理结果
- 最后两种推理结果的差值即为条件干预效应(CATE)的估计值:
$$ \hat{\tau}(x)_i = M_s(X_i, T=1) - M_s(X_i, T=0) $$
S 学习器分析:
- 该方法可以处理连续和离散两种类型的结果,适用性强;是因果效应评估的首选方法,最终性能高度依赖于数据集
- 不适用于干预变量较弱或外生变量维度过高的情况,因为这种情况下干预的作用容易被模型忽略掉
T-Learner
T 学习器(T-Learner)
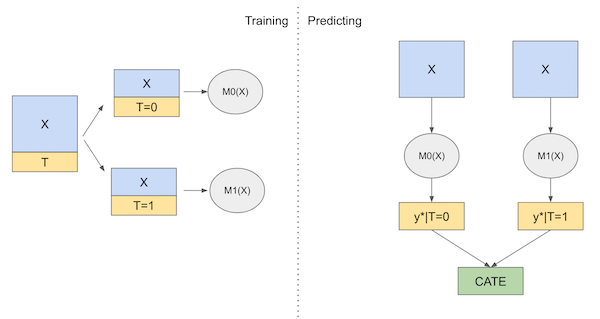
- 先根据是否干预对数据分组,再对两组数据分别建模
- 推理阶段,并根据两个模型的预测结果差值来估计 CATE
$$ \hat{\tau}(x)_i = M_1(X_i) - M_0(X_i) $$ T 学习器分析:
- 解决了 S 学习器中干预变量容易被忽略的问题
- 两组模型独立训练,数据利用率低,存在样本分组引入的偏差,最终预估结果的方差大;该方法仅适用于离散数据,不适用于连续数据
X-Learner
X 学习器(X-Learner)分为两个阶段
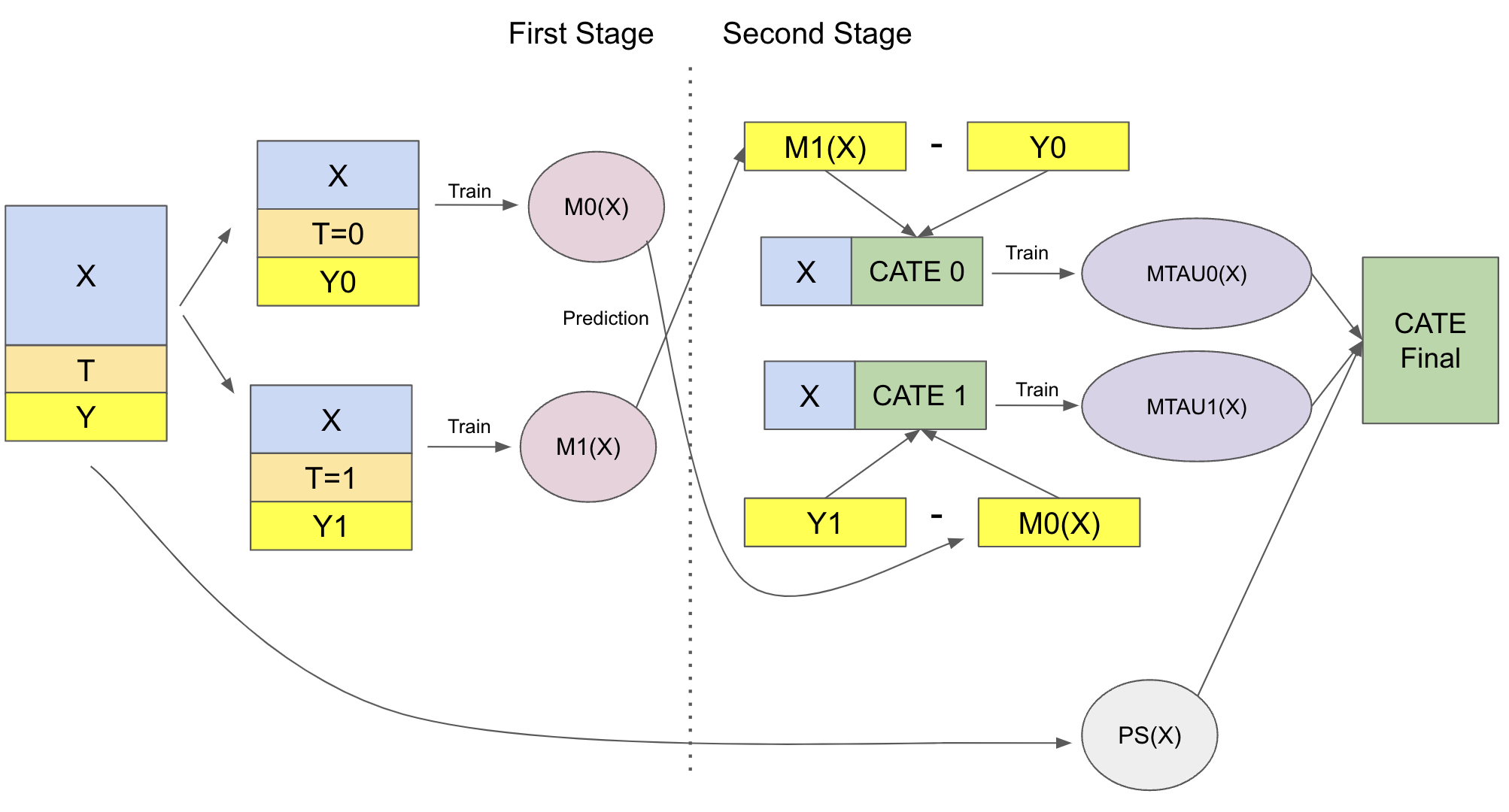
- 第一阶段与 T-learner 相同,也是分组独立训练建模;其中干预组训练的模型为 $\hat{M}_1$,对照组训练的模型为$\hat{M}_0$
- 第二阶段,先将干预组的样本带入 $\hat{M}_0$ 进行推理,得到反事实推论 $\hat{M}_0(X, T=1)$,即不干预后的结果;再和实际的干预效果进行对比,得到干预效应的估计 $\hat{\tau}(X, T=1)$;同理可得对照组的干预效应估计:$$
\begin{align} \hat{\tau}(X, T=0) & = \hat{M}_1(X, T=0) - Y_{T=0} \ \\ \hat{\tau}(X, T=1) &= Y_{T=1} - \hat{M}_0(X, T=1) \end{align} $$
- 然后用估计的干预效应作为目标,进行建模训练,得到了可直接用于 CATE 估计预测的两个新模型 $\hat{M}{\tau 0}(X)$ 和 $\hat{M}{\tau 1}(X)$:
$$ \begin{align} \hat{M}_{\tau 0}(X) \approx E[\hat{\tau}(X)|T=0] \ \\ \hat{M}_{\tau 1}(X) \approx E[\hat{\tau}(X)|T=1] \end{align} $$
- 最后在推理阶段,结合两个新模型的结果,进行更合理的 CATE 估计(其中 $\hat{e}$ 表示权重调节函数,一般考虑用倾向性评分):
$$ \hat{\tau(x)} = \hat{M}_{\tau 0}(X)\hat{e}(x) + \hat{M}_{\tau 1}(X)(1-\hat{e}(x)) $$
X 学习器分析:
- 通过交叉设计来解决干预引起的偏差问题,也能充分地利用数据;还能处理由于对照组和干预组样本量差异引起的数据偏斜问题
- 实现过程较为复杂,其中权重调节函数需要人工调整;该方法仅适用于离散数据,不适用于连续数据