异质性干预效应
定义外生变量为 $X$,干预变量为 $T$,评估异质性干预效应的公式如下: $$ \underset{T}{argmax} \ E[Y|X, T] $$
- 举例来说,$Y$ 可以是每日销售额,$X$ 是背景特征(无法控制的外生变量,比如前几天的平均销售额),而 $T$ 是可以提高销售额的干预变量(比如价格调整、库存水平或营销策略)
- 通过背景特征 $X$ 来定义个体类型,从而实现干预的异质化,即找到针对个体的最佳干预方式
线性回归示例
估计条件平均干预效应(CATE),以线性回归为例: $$ y_i = \beta_0 + \beta_1 t_i + \beta_2 X_i + \beta_3 t_i X_i + e_i $$
- 其中 $\hat{\beta_1} + \hat{\beta_3}X_i$ 描述了结果 $y$ 对干预 $t$ 的敏感度预测,即 CATE
以冰淇淋销量的敏感度预测为例:
- 实验目的:评估价格和温度,对冰淇淋销量的影响
- 定义线性方程:$sales_i = \beta_0 + \beta_1 price_i + \beta_2 price_i * temp_i + \pmb{\beta_3}X_i + e_i$
- 价格对冰淇淋销量的敏感度预测可表示如下:$\hat{\beta_{1}}+\hat{\beta_{2}}temp_{i}$
- 通过回归建模可得,$\hat{\beta_{1}}=-3.6,\hat{\beta_{2}}=0.03$;因此当气温在 25° 时,价格每增加 1 块,销量就会下降 2.8 个单位;但当气温在 35° 时,每增加 1 雷亚尔的价格,销量只会下降 2.5 个单位
- 该结论符合直觉。随着天气越来越热,人们也更愿意为冰淇淋支付更高的价格
非参数机器学习
CATE 也可以通过非参数的机器学习模型来评估
- 构建集成树模型 $G$ ,用于建模预测(假设希望预测销量对价格的敏感度):$sales_{i}=G(X_{i},price_{i})+e_{i}$;其中 $e_{i}$ 表示残差,描述了建模不可知的信息
- 先在测试集上评估模型的结果,确保预测的有效性(比如 $R^2>0.7$)
- 再利用数值近似法,借助模型 $G$ 来评估销量的敏感度:$\frac{y(t+h)-y(t)}{h}$;$h$ 是对 $t$ 的极小扰动,在本例中可取值 $h=0.01$
除了数值近似法,还可以通过目标转换的方式来直接预测 CATE
- 目标转换法(也称 F-Learner)通过将原始目标 $Y$ 与干扰 $T$ 结合,构建转换了一个新的预测目标,并且该目标的期望等于 CATE
- 对于分类问题,目标转换的公式可表示如下:$Y^*_i = Y_i * \dfrac{T_i - e(X_i)}{e(X_i)(1-e(X_i))}$;其中 $e(X_i)$ 表示倾向得分或干预概率;对转换后的目标进行预测建模,得到的模型即可直接用于 CATE 的预测推理
- 对于回归问题,目标转换的相关研究偏少;此处只提供一个在实践中有效但可能缺少严格理论保障的转换方法:$Y^*_i = (Y_i- \bar{Y})\dfrac{(T_i - \bar{T})}{\sigma^2_T}$;其中 $\sigma_T$ 表示干预变量的标准差
- 目标转换法会增加预测结果的方差,因此更适用于数据规模较大(百万级)的情况,并且主要用于分类问题,在回归问题上的研究偏少
关于以上两个转换公式的详细证明过程(转换后目标的期望等于 CATE)可参阅《因果推断:从概念到实践》的第 20 章
其他可用于异质性因果效应评估的常见方法:双重机器学习 DML、双向固定效应 TWFE、 合成双重差分法 SDID、广义随机森林 GRF
因果效应评价
分段的敏感度图 Sensitivity by Model Band:
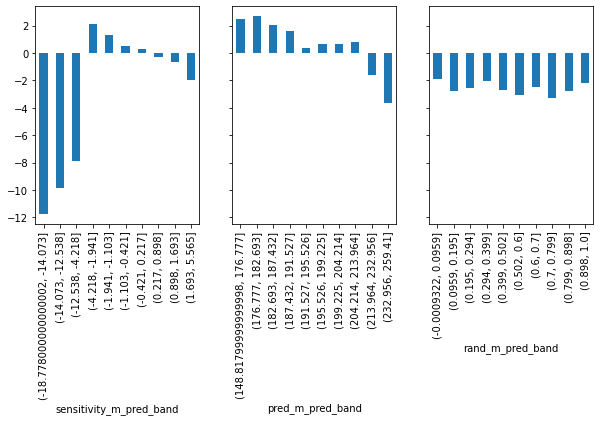
- 根据模型预测输出对样本进行分区,计算每个分区的平均敏感度
累积敏感度曲线 Cumulative Sensitivity Curve:
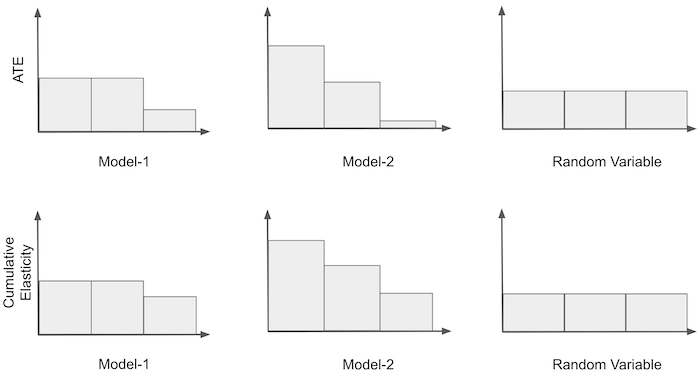
- 对于完全随机样本,不同分组间的 CATE 是一样的,等价于 ATE
- 因此按照分区累积的灵敏度曲线会逐渐收敛并接近随机模型的表现
- 对不同模型来说,累积敏感度曲线越陡峭越好(Model-2 优于 Model-1)
累积增益曲线 Cumulative Gain Curve
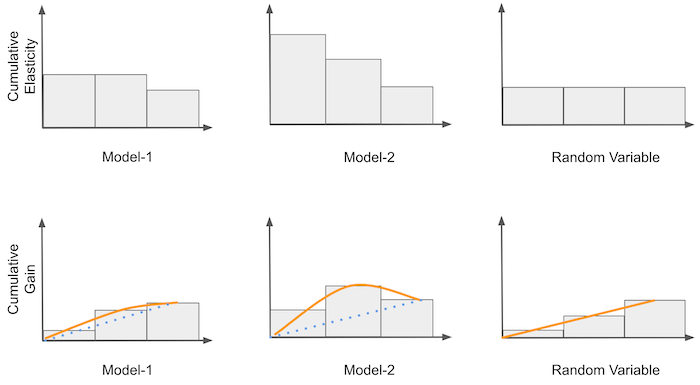
- 在累积敏感度曲线的基础上优化:用累积敏感度乘以比例样本量
- 累积增益曲线与随机曲线的偏差越大,模型越好(Model-2 优于 Model-1)
- 根据回归预测的残差 $\hat\epsilon_i$ 和干预效应值,可为累积增益曲线计算并绘制置信区间
$$ci = s_{\hat\beta_1}=\sqrt{\frac{\sum_i\hat\epsilon_i^2}{(n-2)\sum_i(t_i-\bar t)^2}} $$
Qini 曲线:
- 累积增益曲线的修正版本,解决了干预组和对照组间数据不平衡的问题
- 当干预组和对照组的样本量相同时,Qini 曲线等价于累积增益曲线
累积增益曲线可以看作因果模型的 ROC 曲线,其中累积增益曲线相对随机曲线下面积,也被称为 AUUC(Area Under Uplift Curve);而 Qini 曲线下面积对应的是 Qini 系数